 |
Эйлер Леонард (1707-1783)

См. в Википедии Эйлер, Леонард
Источник - Википедия
Эйлер, Леонард (нем. Leonhard Euler; 15 апреля 1707, Базель, Швейцария — 7
(18) сентября 1783, Санкт-Петербург, Российская империя) — швейцарский,
немецкий и российский математик и механик, внёсший фундаментальный вклад в
развитие этих наук (а также физики, астрономии и ряда прикладных наук).
Эйлер — автор более чем 850 работ (включая два десятка фундаментальных
монографий) по математическому анализу, дифференциальной геометрии, теории
чисел, приближённым вычислениям, небесной механике, математической физике,
оптике, баллистике, кораблестроению, теории музыки и другим областям. Он
глубоко изучал медицину, химию, ботанику, воздухоплавание, теорию музыки,
множество европейских и древних языков. Академик Петербургской, Берлинской,
Туринской, Лиссабонской и Базельской академий наук, иностранный член
Парижской академии наук.
Почти полжизни провёл в России, где внёс существенный вклад в становление
российской науки. В 1726 году он был приглашён работать в Санкт-Петербург,
куда переехал годом позже. С 1726 по 1741, а также с 1766 года был
академиком Петербургской академии наук (будучи сначала адъюнктом, а с 1731
года — профессором); в 1741—1766 годах работал в Берлине (оставаясь
одновременно почётным членом Петербургской академии). Уже через год
пребывания в России он хорошо знал русский язык и часть своих сочинений
(особенно учебники) публиковал на русском. Первые русские
академики-математики (С. К. Котельников) и астрономы (С. Я. Румовский) были
учениками Эйлера. Некоторые из его потомков до сих пор живут в России.
Леонард Эйлер родился в 1707 году в семье базельского пастора Пауля Эйлера,
друга семьи Бернулли, и Маргариты Эйлер, урождённой Брукер. Вскоре после
рождения Леонарда семья переехала в селение Рихен (в часе ходьбы от
Базеля), куда Пауль Эйлер был назначен пастором; там и прошли первые годы
детства мальчика. Начальное обучение Леонард получил дома под руководством
отца (тот в своё время учился математике у
Якоба Бернулли). Пастор готовил старшего
сына к духовной карьере, однако занимался с ним и математикой — как в
качестве развлечения, так и для развития логического мышления, и Леонард
рано проявил математические способности.
Когда Леонард подрос, его перевезли к бабушке в Базель, где он учился в
гимназии (продолжая при этом увлечённо изучать математику). В 1720 году
способного гимназиста допустили к посещению публичных лекций в Базельском
университете; там он обратил на себя внимание профессора Иоганна Бернулли
(младшего брата Якоба Бернулли). Знаменитый учёный передал одарённому
подростку для изучения математические статьи, разрешив при этом для
прояснения трудных мест приходить к нему домой по субботам после
обеда.
20 октября 1720 года 13-летний Леонард Эйлер стал студентом факультета
искусств Базельского университета. Но любовь к математике направила
Леонарда по иному пути. Посещая дом своего учителя, Эйлер познакомился и
подружился с его сыновьями — Даниилом и Николаем, которые также, по
семейной традиции, глубоко изучали математику. В 1723 году Эйлер получил
(по существовавшему в Базельском университете обычаю) первую награду
(primam lauream). 8 июля 1724 года 17-летний Леонард Эйлер произнёс на
латыни речь о сравнении философских воззрений Декарта и Ньютона и был
удостоен учёной степени магистра искусств.
В последующие два года юный Эйлер написал несколько научных работ. Одна из
них, «Диссертация по физике о звуке», была представлена на конкурс для
замещения неожиданно освободившейся в Базельском университете должности
профессора физики (1725). Но, несмотря на положительный отзыв, 19-летнего
Эйлера сочли слишком юным, чтобы включить в число кандидатов на
профессорскую кафедру. Надо отметить, что число научных вакансий в
Швейцарии было совсем невелико. Поэтому братья
Даниил и
Николай Бернулли уехали в Россию, где как раз шла организация Академии
наук; они обещали похлопотать там и о должности для Эйлера.
В начале зимы 1726—1727 гг. Эйлер получил известие из Санкт-Петербурга: по
рекомендации братьев Бернулли он приглашён на должность адъюнкта (помощника
профессора) по кафедре физиологии (эту кафедру занимал Д. Бернулли) с
годовым жалованьем 200 рублей (сохранилось письмо Эйлера президенту
Академии Л. Л. Блюментросту от 9 ноября 1726 г. с благодарностью за
принятие в Академию). Поскольку
Иоганн Бернулли
был известным врачом, то в России считали, что Леонард Эйлер как его
лучший ученик — тоже врач. Свой отъезд из Базеля Эйлер отложил, однако, до
весны, посвятив оставшиеся месяцы серьёзному изучению медицинских наук,
глубоким знанием которых он впоследствии поражал своих современников.
Наконец, 5 апреля 1727 года Эйлер навсегда покинул Швейцарию, хотя
швейцарское (базельское) подданство сохранил до конца жизни.
22 января (2 февраля) 1724 года Пётр I
утвердил проект устройства
Петербургской академии. 28 января (8 февраля) 1724 года вышел указ
Сената о создании Академии. Из 22 профессоров и адъюнктов, приглашённых в
первые годы, оказалось 8 математиков, которые занимались также механикой,
физикой, астрономией, картографией, теорией кораблестроения, службой мер и
весов.
Эйлер (путь которого из Базеля лежал через Любек, Ревель и Кронштадт)
прибыл в Санкт-Петербург 24 мая 1727 года; за несколько дней до этого
умерла императрица
Екатерина I, покровительница Академии,
и учёные пребывали в унынии и растерянности. Эйлеру помогли, однако,
освоиться на новом месте земляки-базельцы: академики Даниил Бернулли и Якоб
Герман; последний, являвшийся профессором по кафедре высшей математики,
доводился молодому учёному дальним родственником и оказывал ему
всевозможное покровительство. Эйлера сделали адъюнктом высшей математики (а
не физиологии, как первоначально планировалось), хотя он в Петербурге
проводил исследования в области гидродинамики биологических жидкостей,
выделили ему жалованье 300 рублей в год и предоставили казённую квартиру.
Ко всеобщему удивлению, он уже в следующем по приезде году стал бегло
говорить по-русски.
В 1728 году началась публикация первого русского научного
журнала «Комментарии Петербургской Академии
наук»
(на латинском языке). Уже второй том содержал три статьи Эйлера, и в
последующие годы практически каждый выпуск академического ежегодника
включал несколько новых его работ. Всего в этом издании было опубликовано
более 400 статей Эйлера.
В сентябре 1730 года закончился срок контрактов, заключённых с академиками
Я. Германом и Г. Б. Бильфингером (последний был профессором по кафедре
экспериментальной и теоретической физики). Их кафедры возглавили
соответственно Даниил Бернулли и Леонард Эйлер; последний получил
увеличение жалованья до 400 рублей, а 22 января 1731 года — и официальную
должность профессора. Ещё через два года (1733) Даниил Бернулли вернулся в
Швейцарию, и Эйлер, оставив кафедру физики, занял его кафедру, став
академиком и профессором высшей математики с окладом 600 рублей (впрочем,
Даниил Бернулли получал вдвое больше).
27 декабря 1733 года 26-летний Леонард Эйлер женился на своей ровеснице
Катарине (нем. Katharina Gsell), дочери
академического живописца Георга Гзеля (петербургского швейцарца).
Молодожёны приобрели дом на набережной Невы, где и поселились. В семье
Эйлера родились 13 детей, но выжили 3 сына и 2 дочери.
Работы у молодого профессора было много: картография, всевозможные
экспертизы, консультации для кораблестроителей и артиллеристов, составление
учебных руководств, проектирование пожарных насосов и т. д. От него даже
требовали составления гороскопов, каковой заказ Эйлер со всем возможным
тактом переадресовал штатному астроному. А. С. Пушкин приводит
романтический рассказ: якобы Эйлер составил гороскоп для новорождённого
Иоанна Антоновича (1740), но результат его настолько испугал, что он никому
не стал его показывать и лишь после смерти несчастного царевича рассказал о
нём графу К. Г. Разумовскому. Достоверность этого исторического анекдота
крайне сомнительна.
За первый период пребывания в России он написал более 90 крупных научных
работ. Значительная часть академических «Записок» заполнена трудами Эйлера.
Он делал доклады на научных семинарах, читал публичные лекции, участвовал в
выполнении различных технических заказов правительственных ведомств. В
течение 1730-х годов Эйлер возглавлял работу по
картографированию Российской
империи, которая (уже после отъезда Эйлера, в 1745 году) завершилась
изданием атласа территории страны. Как рассказывал Н. И. Фусс, в 1735 году
Академия получила задание выполнить срочное и очень громоздкое
математическое вычисление, причём группа академиков просила на это три
месяца, а Эйлер взялся выполнить работу за 3 дня — и справился
самостоятельно; однако перенапряжение не прошло бесследно: он заболел и
потерял зрение на правый глаз. Впрочем, сам Эйлер в одном из своих писем
приписывал потерю глаза своей работе по составлению карт в географическом
департаменте при Академии.
Двухтомное сочинение «Механика, или наука о движении, изложенная
аналитически», изданное в 1736 году, принесло Эйлеру общеевропейскую
известность. В этой монографии Эйлер с успехом применил методы
математического анализа к общему решению проблем движения в пустоте и в
сопротивляющейся среде.
Одной из важнейших задач Академии стала подготовка отечественных кадров,
для чего при Академии были созданы университет и гимназия. В силу острой
нехватки учебников на русском языке Академия обратилась к своим членам с
просьбой составить такие руководства. Эйлер составил на немецком языке
очень добротное «Руководство к арифметике», которое тут же было переведено
на русский и служило не один год в качестве начального учебника. Перевод
первой части выполнил в 1740 году первый русский адъюнкт Академии, ученик
Эйлера
Василий Адодуров.
Обстановка ухудшилась, когда в 1740 году умерла императрица
Анна Иоанновна, и императором был
объявлен малолетний Иоанн VI. «Предвиделось нечто опасное, — писал позднее
Эйлер в автобиографии. — После кончины достославной императрицы Анны при
последовавшем тогда регентстве… положение начало представляться
неуверенным». В самом деле, в регентство
Анны Леопольдовны Петербургская
академия окончательно пришла в запустение. Эйлер стал обдумывать вариант
возврата на родину или переезда в иную страну. В конце концов он принял
предложение прусского короля
Фридриха, который приглашал его на
весьма выгодных условиях в Берлинскую академию, на должность директора её
Математического департамента. Академия создавалась на базе прусского
Королевского общества, основанного ещё Лейбницем, но в те годы
находившегося в удручающем состоянии.
Эйлер подал руководству Петербургской академии прошение об отставке:
Того ради нахожусь принужден, как ради слабого здоровья, так и других
обстоятельств, искать приятнейшего климата и принять от его Королевского
Величества Прусского учиненное мне призывание. Того ради прошу
Императорскую Академию наук всеподданнейше меня милостиво уволить и
снабдить для моего и домашних моих проезду потребным пашпортом.
29 мая 1741 года разрешение Академии было получено. Эйлер был «отпущен» и
утверждён почётным членом Академии с окладом 200 рублей. В июне 1741 года
34-летний Леонард Эйлер с женой, двумя сыновьями и четырьмя племянниками
прибыл в
Берлин. Он провёл там 25 лет и
издал около 260 работ.
Первое время Эйлера принимали в Берлине доброжелательно, даже приглашали на
придворные балы. Маркиз Кондорсе вспоминал, что вскоре после переезда в
Берлин Эйлера пригласили на придворный бал. На вопрос королевы-матери,
отчего он так немногословен, Эйлер ответил: «Я приехал из страны, где, кто
разговаривает, того вешают».
Работы у Эйлера было немало. Помимо математических исследований, он
руководил обсерваторией, занимался многими практическими делами, включая
выпуск календарей (основной источник дохода Академии), чеканку прусских
монет, прокладку нового водопровода, организацию пенсионного обеспечения и
лотерей.
В 1742 году вышло четырёхтомное собрание сочинений Иоганна Бернулли.
Посылая его из Базеля Эйлеру в Берлин, старый учёный писал своему ученику:
«Я посвятил себя детству высшей математики. Ты, мой друг, продолжишь её
становление в зрелости». В берлинский период, одна за другой, выходят
работы Эйлера: «Введение в анализ бесконечно малых» (1748), «Морская наука»
(1749), «Теория движения Луны» (1753), «Наставление по дифференциальному
исчислению» (лат. Institutiones calculi differentialis, 1755).
Многочисленные статьи по отдельным вопросам печатаются в изданиях
Берлинской и Петербургской Академий. В 1744 году Эйлер открыл вариационное
исчисление. В его работах используются продуманная терминология и
математическая символика, в значительной степени сохранившиеся до наших
дней, изложение доводится до уровня практических алгоритмов.
Все годы пребывания в Германии Эйлер сохранял связь с Россией. Эйлер
участвовал в публикациях Петербургской Академии, приобретал для неё книги и
инструменты, редактировал математические отделы русских журналов. На его
квартире, на полном пансионе, годами жили молодые русские учёные,
командированные на стажировку. Известно об оживлённой переписке Эйлера с М.
В. Ломоносовым, в творчестве которого он высоко ценил «счастливое сочетание
теории с экспериментом». В 1747 году он дал благоприятный отзыв президенту
Академии наук графу К. Г. Разумовскому о статьях Ломоносова по физике и
химии, утверждая:
Все сии диссертации не токмо хороши, но и весьма превосходны, ибо он
[Ломоносов] пишет о материях физических и химических весьма нужных, которые
по ныне не знали и истолковать не могли самые остроумные люди, что он
учинил с таким успехом, что я совершенно уверен в справедливости его
изъяснений. При сём случае г. Ломоносову должен отдать справедливость, что
имеет превосходное дарование для изъяснения физических и химических
явлений. Желать должно, чтоб и другия Академии в состоянии были произвести
такия откровения, как показал г. Ломоносов.
Этой высокой оценке не помешало даже то, что Ломоносов математических работ
не писал и высшей математикой не владел.
Мать известила Эйлера о смерти в Швейцарии его отца (1745); вскоре она
переехала к Эйлеру (скончалась в 1761 году). В 1753 году Эйлер купил
поместье в Шарлоттенбурге
(пригород Берлина) с садом и участком, где разместил свою многочисленную
семью.
По отзывам современников, Эйлер всю жизнь оставался скромным,
жизнерадостным, чрезвычайно отзывчивым человеком, всегда готовым помочь
другому. Однако отношения с королём не сложились: Фридрих находил нового
математика невыносимо скучным, совершенно не светским и обращался с ним
пренебрежительно. В 1759 году умер Мопертюи, президент Берлинской Академии
наук и друг Эйлера. Пост президента Академии король Фридрих II предложил
Д’Аламберу, но тот отказался. Фридрих, недолюбливавший Эйлера, всё же
поручил ему руководство Академией, однако без титула президента.
Во время Семилетней войны
(1756—1763) русская артиллерия разрушила дом Эйлера; узнав об этом,
фельдмаршал Салтыков немедленно возместил потери, а позже императрица
Елизавета прислала от себя ещё 4000
рублей.
В 1765 году опубликована «Теория движения твёрдых тел», а годом позже —
«Элементы вариационного исчисления». Именно здесь впервые появилось
название нового раздела математики, созданного Эйлером и Лагранжем.
В 1762 году на русский престол вступила
Екатерина
II, которая осуществляла политику просвещённого абсолютизма. Хорошо
понимая значение науки как для прогресса государства, так и для
собственного престижа, она провела ряд важных, благоприятных для науки
преобразований в системе народного просвещения и культуры. Императрица
предложила Эйлеру управление математическим классом, звание
конференц-секретаря Академии и оклад 1800 рублей в год. «А если не
понравится, — говорилось в письме её представителю, — благоволит сообщить
свои условия, лишь бы не медлил приездом в Петербург».
Эйлер сообщил в ответ свои условия:
оклад 3000 рублей в год и пост вице-президента Академии;
квартира, свободная от солдатского постоя;
оплачиваемые должности для троих его сыновей, в том числе пост секретаря
Академии для старшего.
Все эти условия были приняты. 6 января 1766 года Екатерина сообщила графу
Воронцову:
Письмо к Вам г. Эйлера доставило мне большое удовольствие, потому что я
узнаю из него о желании его снова вступить в мою службу. Конечно, я нахожу
его совершенно достойным желаемого звания вице-президента Академии наук, но
для этого следует принять некоторые меры, прежде чем я установлю это звание
— говорю установлю, так как доныне его не существовало. При настоящем
положении дел там нет денег на жалование в 3000 рублей, но для человека с
такими достоинствами, как г. Эйлер, я добавлю к академическому жалованию из
государственных доходов, что вместе составит требуемые 3000 рублей… Я
уверена, что моя Академия возродится из пепла от такого важного
приобретения, и заранее поздравляю себя с тем, что возвратила России
великого человека.
Позже Эйлер выдвинул ещё ряд условий (ежегодная пенсия в 1000 рублей жене
после его смерти, компенсация путевых издержек, место для сына-медика и чин
для самого Эйлера). Екатерина удовлетворила и эти условия Эйлера за
исключением требования о чине, отшутившись: «Я дала бы ему, когда он хочет,
чин… (в черновике письма на французском зачеркнуто — коллежского
советника), если бы не опасалась, что этот чин сравняет его со множеством
людей, которые не стоят г. Эйлера. Поистине, его известность лучше чина для
оказания ему должного уважения».
Эйлер подал королю прошение об увольнении со службы, но никакого ответа не
получил. Подал повторно — но Фридрих не желал даже обсуждать вопрос о его
отъезде. Решающую поддержку Эйлеру оказали настойчивые ходатайства
российского представительства от имени императрицы. 2 мая 1766 года Фридрих
наконец-то разрешил великому учёному покинуть Пруссию, не удержавшись,
впрочем, в своей переписке от злобных острот в адрес Эйлера (так, 25 июля
он писал Даламберу: «Господин Эйлер, до безумия любящий Большую и Малую
Медведицу, приблизился к северу для большего удобства к наблюдению их»).
Правда, служившего подполковником артиллерии (нем. Oberstleutnant) Кристофа
— младшего сына Эйлера — король наотрез отказался отпустить из армии;
позднее, благодаря заступничеству Екатерины II, тот всё же смог
присоединиться к отцу и дослужился в русской армии до генерал-лейтенанта.
Летом 1766 года Эйлер вернулся в Россию — теперь уже навсегда.
17 (28) июля 1766 года 60-летний Эйлер, его семья и домочадцы (всего 18
человек) прибыли в российскую столицу. Сразу же по прибытии он был принят
императрицей. Екатерина II встретила его как августейшую особу и осыпала
милостями: пожаловала 8000 рублей на покупку дома на Васильевском острове и
на приобретение обстановки, предоставила на первое время одного из своих
поваров и поручила подготовить соображения о реорганизации Академии.
К несчастью, после возвращения в Петербург у Эйлера образовалась катаракта
левого глаза — он перестал видеть. Вероятно, по этой причине обещанный пост
вице-президента Академии он так и не получил (что не помешало Эйлеру и его
потомкам в течение почти ста лет участвовать в управлении Академией).
Однако слепота не отразилась на работоспособности учёного, он лишь заметил,
что теперь будет меньше отвлекаться от занятий математикой. До обретения
секретаря Эйлер диктовал свои труды мальчику-портному, который всё
записывал по-немецки. Число опубликованных им работ даже возросло; в
течение второго пребывания в России Эйлер продиктовал более 400 статей и 10
книг, что составляет больше половины его творческого наследия.
В 1768—1770 годах вышла в свет двухтомная классическая монография
«Универсальная арифметика» (издавалась также под названиями «Начала
алгебры» и «Полный курс алгебры»). Вначале этот труд был опубликован на
русском языке (1768—1769), издание на немецком вышло два года спустя. Книга
была переведена на многие языки и переиздавалась около 30 раз (трижды — на
русском). Все последующие учебники алгебры создавались под сильнейшим
влиянием книги Эйлера.
В эти же годы вышли трёхтомник «Диоптрика» (лат. Dioptrica, 1769—1771) о
линзовых системах и фундаментальное «Интегральное исчисление» (лат.
Institutiones calculi integralis, 1768—1770), тоже в 3 томах.
Огромную популярность приобрели в XVIII веке, а отчасти и в XIX,
эйлеровские «Письма о разных физических и философических материях,
написанные к некоторой немецкой принцессе…» (1768), которые выдержали свыше
40 изданий на 10 языках (в том числе 4 издания на русском). Это была
научно-популярная энциклопедия широкого охвата, написанная ярко и
общедоступно.
В 1771 году в жизни Эйлера произошли два серьёзных события. В мае в
Петербурге случился большой пожар,
уничтоживший сотни зданий, в том числе дом и почти всё имущество Эйлера.
Самого учёного с трудом спасли. Все рукописи удалось уберечь от огня;
сгорела лишь часть «Новой теории движения луны», но она быстро была
восстановлена с помощью самого Эйлера, сохранившего до глубокой старости
феноменальную память. Эйлеру пришлось временно переселиться в другой дом.
Второе событие: в сентябре того же года, по особому приглашению
императрицы, в Санкт-Петербург прибыл для лечения Эйлера известный немецкий
окулист барон Вентцель. После осмотра он согласился сделать Эйлеру операцию
и удалил с левого глаза катаракту. Эйлер снова стал видеть. Врач предписал
беречь глаз от яркого света, не писать, не читать — лишь постепенно
привыкать к новому состоянию. Однако уже через несколько дней после
операции Эйлер снял повязку и вскоре потерял зрение снова. На этот раз —
окончательно.
1772: «Новая теория движения Луны». Эйлер наконец завершил свой многолетний
труд, приближённо решив задачу трёх тел.
В 1773 году по рекомендации Даниила Бернулли в Петербург приехал из Базеля
ученик Бернулли, Николаус Фусс. Это было большой удачей для Эйлера. Фусс,
одарённый математик, сразу же после приезда взял на себя заботы о
математических трудах Эйлера. Вскоре Фусс женился на внучке Эйлера. В
последующие десять лет — до самой своей смерти — Эйлер преимущественно ему
диктовал свои труды, хотя иногда пользовался «глазами старшего сына» и
других своих учеников. В этом же 1773 году умерла жена Эйлера, с которой он
прожил почти 40 лет. Смерть жены была болезненным ударом для учёного,
искренне привязанного к семье. Вскоре Эйлер женился на
Саломее-Абигайль, сводной сестре
покойной жены.
В 1779 году опубликована «Всеобщая сферическая тригонометрия», это первое
полное изложение всей системы сферической тригонометрии
Эйлер активно трудился до последних дней. В сентябре 1783 года 76-летний
учёный стал ощущать головные боли и слабость. 7 (18) сентября после обеда,
проведённого в кругу семьи, беседуя с академиком А. И. Лекселем о недавно
открытой планете Уран и её орбите, он внезапно почувствовал себя плохо.
Эйлер успел произнести: «Я умираю», — и потерял сознание. Через несколько
часов, так и не приходя в сознание, он скончался от кровоизлияния в
мозг.
«Он перестал вычислять и жить», — сказал Кондорсе на траурном заседании
Парижской Академии наук (фр. Il cessa de calculer et de vivre).
Его похоронили на Смоленском лютеранском кладбище в Петербурге. Надпись на
памятнике на немецком языке гласила: «Здесь покоятся останки знаменитого во
всём свете Леонарда Эйлера, мудреца и праведника. Родился в Базеле 4 апреля
1707 года, умер 7 сентября 1783 года». По смерти Эйлера его могила
затерялась и была найдена, в заброшенном состоянии, только в 1830 году. В
1837 году Академия наук заменила эту надгробную плиту новым гранитным
надгробием (существующим и поныне) с надписью на латинском языке «Леонарду
Эйлеру — Петербургская Академия» (лат. Leonhardo Eulero — Academia
Petropolitana).
В ходе празднования 250-летия Эйлера (1957 год) прах великого математика
был перенесён в «Некрополь XVIII века» на Лазаревском кладбище
Александро-Невской лавры, где располагается поблизости от могилы М. В.
Ломоносова.
Эйлер оставил важнейшие труды по самым различным отраслям математики,
механики, физики, астрономии и по ряду прикладных наук. Познания Эйлера
были энциклопедичны; кроме математики, он глубоко изучал ботанику,
медицину, химию, теорию музыки, множество европейских и древних
языков.
Эйлер охотно участвовал в научных дискуссиях, из которых наибольшую
известность получили:
спор о струне;
спор с Д’Аламбером о свойствах комплексного логарифма;
спор с Джоном Доллондом о том, возможно ли создать ахроматическую
линзу.
Во всех упомянутых случаях позиция Эйлера поддержана современной
наукой.
С точки зрения математики, XVIII век — это век Эйлера. Если до него
достижения в области математики были разрознены и не всегда согласованы, то
Эйлер впервые увязал анализ, алгебру, геометрию, тригонометрию, теорию
чисел и другие дисциплины в единую систему, добавив при этом немало
собственных открытий. Значительная часть математики преподаётся с тех пор
«по Эйлеру» почти без изменений.
Благодаря Эйлеру в математику вошли общая теория рядов, фундаментальная
«формула Эйлера» в теории комплексных чисел, операция сравнения по целому
модулю, полная теория непрерывных дробей, аналитический фундамент механики,
многочисленные приёмы интегрирования и решения дифференциальных уравнений,
число e, обозначение i для мнимой единицы, ряд специальных функций и многое
другое.
По существу, именно он создал несколько новых математических дисциплин —
теорию чисел, вариационное исчисление, теорию комплексных функций,
дифференциальную геометрию поверхностей; он заложил основы теории
специальных функций. Другие области его трудов: диофантов анализ,
математическая физика, статистика и т. д.
Биографы отмечают, что Эйлер был виртуозным алгоритмистом. Он неизменно
старался довести свои открытия до уровня конкретных вычислительных методов
и сам был непревзойдённым мастером численных расчётов. Ж. Кондорсе
рассказывал, что однажды два студента, выполняя независимо сложные
астрономические вычисления, получили немного различающиеся результаты в
50-м знаке и обратились к Эйлеру за помощью. Эйлер проделал те же
вычисления в уме и указал правильный результат.
П. Л. Чебышёв писал: «Эйлером было положено начало всех изысканий,
составляющих общую теорию чисел». Большинство математиков XVIII века
занимались развитием анализа, но Эйлер пронёс увлечение древней арифметикой
через всю свою жизнь. Благодаря его трудам интерес к теории чисел к концу
века возродился.
Эйлер продолжил исследования Ферма, ранее высказавшего (под влиянием
Диофанта) ряд разрозненных гипотез о натуральных числах. Эйлер строго
доказал эти гипотезы, значительно обобщил их и объединил в содержательную
теорию чисел. Он ввёл в математику исключительно важную «функцию Эйлера» и
сформулировал с её помощью «теорему Эйлера». Он опроверг гипотезу Ферма о
том, что все числа вида {\displaystyle F_{n}=2^{2^{n}}+1} — простые;
оказалось, что {\displaystyle F_{5}} делится на 641. Доказал утверждение
Ферма о представлении нечётного простого числа в виде суммы двух квадратов.
Дал одно из решений задачи о четырёх кубах. Доказал, что число Мерсенна
{\displaystyle 2^{31}-1=2147483647} — простое число; в течение почти ста
лет (до 1867 года) оно оставалось наибольшим известным простым числом.
Эйлер создал основу теории сравнений и квадратичных вычетов, указав для
последних критерий разрешимости. Эйлер ввёл понятие первообразного корня и
выдвинул гипотезу, что для любого простого числа p существует первообразный
корень по модулю p; доказать это он не сумел, позднее теорему доказали
Лежандр и Гаусс. Большое значение в теории имела другая гипотеза Эйлера —
квадратичный закон взаимности, также доказанный Гауссом. Эйлер доказал
Великую теорему Ферма для {\displaystyle n=3} и {\displaystyle n=4} ,
создал полную теорию непрерывных дробей, исследовал различные классы
диофантовых уравнений, теорию разбиений чисел на слагаемые.
В задаче о количестве разбиений натурального числа {\displaystyle n}
получил формулу, выражающую производящую функцию числа разбиений
{\displaystyle p(n)} через бесконечное произведение
{\displaystyle \sum _{n=0}^{\infty }p(n)x^{n}=\prod _{k=1}^{\infty }{\frac
{1}{1-x^{k}}}}
Эйлер определил дзета-функцию, обобщение которой получило впоследствии имя
Римана:
{\displaystyle \zeta (s)={\frac {1}{1^{s}}}+{\frac {1}{2^{s}}}+{\frac
{1}{3^{s}}}+\ldots }
где {\displaystyle \displaystyle s} вещественное число (у Римана —
комплексное). Эйлер вывел для неё разложение:
{\displaystyle \zeta (s)=\prod _{p}{\frac {1}{1-p^{-s}}}}
где произведение берётся по всем простым числам {\displaystyle
\displaystyle p} . Тем самым он открыл, что в теории чисел возможно
применение методов математического анализа, положив начало аналитической
теории чисел, в основе которой лежат тождество Эйлера и общий метод
производящих функций.
Одна из главных заслуг Эйлера перед наукой — монография «Введение в анализ
бесконечно малых» (1748). В 1755 году вышло дополненное «Дифференциальное
исчисление», а в 1768—1770 годах — три тома «Интегрального исчисления». В
совокупности это фундаментальный, хорошо иллюстрированный примерами курс, с
продуманной терминологией и символикой. «Можно с уверенностью сказать, что
добрая половина того, что преподаётся теперь в курсах высшей алгебры и
высшего анализа, находится в трудах Эйлера» (Н. Н. Лузин). Эйлер первый дал
систематическую теорию интегрирования и используемых при этом технических
приёмов. В частности, он — автор классического способа интегрирования
рациональных функций путём разложения их на простые дроби и метода решения
дифференциальных уравнений произвольного порядка с постоянными
коэффициентами. Впервые ввёл двойные интегралы.
Эйлер всегда уделял особое внимание методам решения дифференциальных
уравнений — как обыкновенных, так и в частных производных, открыв и описав
важные классы интегрируемых дифференциальных уравнений. Изложил «метод
ломаных» Эйлера (1768) — численный метод решения систем обыкновенных
дифференциальных уравнений. Одновременно с А. К. Клеро Эйлер вывел условия
интегрируемости линейных дифференциальных форм от двух или трёх переменных
(1739). Получил серьёзные результаты в теории эллиптических функций, в том
числе первые теоремы сложения эллиптических интегралов (1761). Впервые
исследовал максимумы и минимумы функций многих переменных.
Основание натуральных логарифмов было известно ещё со времён Непера и Якоба
Бернулли, однако Эйлер выполнил настолько глубокое исследование этой
важнейшей константы, что с тех пор она носит его имя. Другая исследованная
им константа: постоянная Эйлера — Маскерони.
Современное определение показательной, логарифмической и тригонометрических
функций — тоже его заслуга, так же как и их символика и обобщение на
комплексный случай. Формулы, часто именуемые в учебниках «условия Коши —
Римана», более правильно было бы назвать «условиями Даламбера —
Эйлера».
Он делит с Лагранжем честь открытия вариационного исчисления, выписав
уравнения Эйлера — Лагранжа для общей вариационной задачи. В 1744 году
Эйлер опубликовал трактат «Метод нахождения кривых линий…» — первую работу
по вариационному исчислению (помимо прочего, она содержала первое
систематическое изложение теории упругих кривых и результаты по
сопротивлению материалов).
Эйлер значительно продвинул теорию рядов и распространил её на комплексную
область, получив при этом знаменитую формулу Эйлера, дающую
тригонометрическое представление комплексного числа. Большое впечатление на
математический мир произвели ряды, впервые просуммированные Эйлером, в том
числе не поддававшийся до него никому ряд обратных квадратов:
{\displaystyle \zeta (2)=\lim _{n\to \infty }\left({\frac
{1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+\cdots +{\frac
{1}{n^{2}}}\right)={\frac {\pi ^{2}}{6}}}
С помощью рядов Эйлер исследовал трансцендентные функции, то есть те
функции, которые не выражаются алгебраическим уравнением (например,
интегральный логарифм). Он открыл (1729—1730) имеющие сейчас многообразные
приложения «эйлеровы интегралы» —специальные функции, вошедшие в науку как
гамма-функция и бета-функция Эйлера. При решении задачи о колебаниях
упругой мембраны (возникла в связи с определением высоты звука литавр)
Эйлер в 1764 году впервые ввёл бесселевы функции для любого натурального
индекса (исследование Ф. В. Бесселя, имя которого эти функции носят ныне,
относится к 1824 году).
С более поздней точки зрения, действия Эйлера с бесконечными рядами не
всегда могут считаться корректными (обоснование анализа было проведено лишь
полвека спустя), но феноменальная математическая интуиция практически
всегда подсказывала ему правильный результат. Вместе с тем во многих важных
отношениях его понимание опередило время — например, предложенное им
обобщённое понимание суммы расходящихся рядов и операций с ними послужило
основой современной теории этих рядов, развитой в конце XIX — начале XX
века.
В элементарной геометрии Эйлер обнаружил несколько фактов, не отмеченных
Евклидом:
три высоты треугольника пересекаются в одной точке (ортоцентре);
в треугольнике ортоцентр H, центр описанной окружности U и центр тяжести S
(он же — центроид) лежат на одной прямой — «прямой Эйлера» e (см. рисунок
справа). Уточнение. На «прямой Эйлера» также лежит центр окружности Эйлера
(центр окружности девяти точек) (см. другой рисунок);
основания трёх высот произвольного треугольника, середины трёх его сторон и
середины трёх отрезков, соединяющих его вершины с ортоцентром, лежат все на
одной окружности («окружности Эйлера»);
число вершин (В), граней (Г) и рёбер (Р) у любого выпуклого многогранника
связаны простой формулой: {\displaystyle \mathrm {B} -\mathrm {P} +\Gamma
\;=\;2} (в современной трактовке число 2 здесь выступает как важнейший
топологический инвариант выпуклого многогранника — его эйлерова
характеристика, а сам этот результат Эйлера, полученный в 1758 году,
положил начало накоплению фактов топологии).
Второй том «Введения в анализ бесконечно малых» (1748) — это первый в мире
учебник по аналитической геометрии и основам дифференциальной геометрии.
Эйлер дал классификацию алгебраических кривых 3-го и 4-го порядков, а также
поверхностей второго порядка. Термин «аффинные преобразования» впервые
введён в этой книге вместе с теорией таких преобразований. В 1732 году
Эйлер вывел общее уравнение геодезических линий на поверхности.
В 1760 году вышли фундаментальные «Исследования о кривизне поверхностей».
Эйлер обнаружил, что в каждой точке гладкой поверхности имеются два
нормальных сечения с минимальным и максимальным радиусами кривизны и что
плоскости их взаимно перпендикулярны. Вывел формулу связи кривизны сечения
поверхности с главными кривизнами.
В 1771 году Эйлер опубликовал сочинение «О телах, поверхность которых можно
развернуть на плоскость». В этой работе введено понятие развёртывающейся
поверхности, то есть поверхности, которая может быть наложена на плоскость
без складок и разрывов. Эйлер, однако, даёт здесь вполне общую теорию
метрики, от которой зависит вся внутренняя геометрия поверхности. Позже
исследование метрики становится у него основным инструментом теории
поверхностей.
В связи с задачами картографии Эйлер глубоко исследовал конформные
отображения, впервые применив для этого средства комплексного анализа.
Эйлер много внимания уделял представлению натуральных чисел в виде сумм
специального вида и сформулировал ряд теорем для вычисления числа
разбиений. При решении комбинаторных задач он глубоко изучил свойства
сочетаний и перестановок, ввёл в рассмотрение числа Эйлера.
Эйлер исследовал алгоритмы построения магических квадратов методом обхода
шахматным конём. Две его работы (1776, 1779) заложили фундамент общей
теории латинских и греко-латинских квадратов, огромная практическая
ценность которой выяснилась после создания Рональдом Фишером методов
планирования эксперимента, а также в теории кодов, исправляющих
ошибки.
Статья Эйлера 1736 года «Решение вопроса, связанного с геометрией
положения» положила начало теории графов как математической дисциплине.
Поводом для исследования послужила задача о семи мостах Кёнигсберга: можно
ли пройти каждый мост по одному разу и вернуться в исходное место? Эйлер
формализовал её, сведя к задаче о существовании в графе (вершины которого
отвечают частям города, разделённым протоками реки Преголя, а рёбра —
мостам) циклического маршрута, проходящего по каждому ребру ровно один раз
(в современной терминологии — эйлерова цикла). Решая последнюю задачу,
Эйлер показал: для наличия эйлерова цикла в графе нужно, чтобы у каждой
вершины её степень (число выходящих из вершины рёбер) была чётной (а в
задаче о кёнигсбергских мостах это не так: степени равны 3, 3, 3 и 5).
Эйлер внёс существенный вклад в теорию и методы приближённых вычислений.
Впервые применил аналитические методы в картографии. Предложил удобный
метод графического изображения соотношений и операций над множествами,
получивший название «Круги Эйлера» (или Эйлера-Венна).
Множество работ Эйлера посвящены различным разделам механики и физики. По
поводу ключевой роли Эйлера на этапе оформления механики в точную науку К.
Трусделл писал: «Механика, как её сегодня преподают инженерам и
математикам, является в значительной степени его творением».
В 1736 году вышел двухтомный трактат Эйлера «Механика, или наука о
движении, в аналитическом изложении», знаменовавший новый этап в развитии
этой древней науки и посвящённый динамике материальной точки. В отличие от
основоположников данного раздела динамики — Галилея и Ньютона,
пользовавшихся геометрическими методами, 29-летний Эйлер предложил
регулярный и единообразный аналитический метод решения различных задач
динамики: составление дифференциальных уравнений движения материального
объекта и их последующее интегрирование при заданных начальных
условиях.
В первом томе трактата рассматривается движение свободной материальной
точки, во втором — несвободной, причём исследуется движение как в пустоте,
так и в сопротивляющейся среде. Отдельно рассматриваются задачи баллистики
и теория маятника. Здесь Эйлер впервые записывает дифференциальное
уравнение прямолинейного движения точки, а для общего случая криволинейного
её движения вводит естественные уравнения движения — уравнения в проекциях
на оси сопровождающего трёхгранника. Во многих конкретных задачах он
доводит интегрирование уравнений движения до конца; в случаях движения
точки без сопротивления он систематически пользуется первым интегралом
уравнений движения — интегралом энергии. Во втором томе, в связи с
проблемой движения точки по произвольно искривлённой поверхности,
излагается созданная Эйлером дифференциальная геометрия поверхностей.
К динамике материальной точки Эйлер возвращался и позднее. В 1746 году,
исследуя движение материальной точки по подвижной поверхности, он приходит
(одновременно с Д. Бернулли и П. Дарси) к теореме об изменении момента
количества движения. В 1765 году Эйлер, использовав выдвинутую в 1742 году
К. Маклореном идею о разложении скоростей и сил по трём неподвижным
координатным осям, впервые записывает дифференциальные уравнения движения
материальной точки в проекциях на декартовы неподвижные оси.
Последний результат был опубликован Эйлером в его втором фундаментальном
трактате по аналитической динамике — книге «Теория движения твёрдых тел»
(1765). Основное её содержание посвящено, однако, другому разделу механики
— динамике твёрдого тела, основоположником которого и стал Эйлер. В
трактате, в частности, содержится вывод системы из шести дифференциальных
уравнений движения свободного твёрдого тела. Важное значение для статики
имеет излагаемая в § 620 трактата теорема о приведении приложенной к
твёрдому телу системы сил к двум силам. Проектируя на координатные оси
условия равенства этих сил нулю, Эйлер впервые получает уравнения
равновесия твёрдого тела под действием произвольной пространственной
системы сил.
В трактате 1765 года изложен и ряд фундаментальных результатов Эйлера,
относящихся к кинематике твёрдого тела (в XVIII веке кинематикуещё не
выделяли в качестве отдельного раздела механики). Среди них выделим формулы
Эйлера для распределения скоростей точек абсолютно твёрдого тела (векторный
эквивалент этих формул — кинематическая формула Эйлера) и кинематические
уравнения Эйлера, дающие выражение производных от углов Эйлера (введены им
в 1748 году; в механике применяются для задания ориентации твёрдого тела)
через проекции угловой скорости на оси координат.
Помимо данного трактата, для динамики твёрдого тела важное значение имеют
две более ранние работы Эйлера: «Исследования о механическом познании тел»
и «Вращательное движение твёрдых тел вокруг переменной оси», которые были
представлены на рассмотрение Берлинской академии наук в 1758 году, но
опубликованы в её «Записках» позже (в том же 1765 году, что и трактат). В
них: разработана теория моментов инерции (в частности, впервые доказана
«теорема Гюйгенса — Штейнера»); установлено существование у любого твёрдого
тела с неподвижной точкой по крайней мере трёх осей свободного вращения;
получены динамические уравнения Эйлера, описывающие динамику твёрдого тела
с неподвижной точкой; приведено аналитическое решение данных уравнений в
случае равенства нулю главного момента внешних сил (случай Эйлера) — один
из трёх общих случаев интегрируемости в задаче о динамике тяжёлого твёрдого
тела с неподвижной точкой.
В статье «Общие формулы для произвольного перемещения твёрдого тела» (1775)
Эйлер формулирует и доказывает фундаментальную теорему вращения Эйлера, по
которой произвольное перемещение абсолютно твёрдого тела с неподвижной
точкой представляет собой поворот на некоторый угол вокруг той или иной
оси, проходящей через неподвижную точку.
Эйлеру принадлежит заслуга аналитического оформления принципа наименьшего
действия (предложенного в 1744 году — в весьма нечёткой форме — П. Л.
Мопертюи), правильного понимания условий применимости принципа и его
первого доказательства (проведённого в том же 1744 году для случая одной
материальной точки, движущейся под действием центральной силы). Под
действием здесь (речь идёт о так называемом укороченном действии, а не о
действии по Гамильтону) применительно к системе материальных точек
понимается интеграл
{\displaystyle W\;=\;\int \limits _{A}^{B}\,\sum
_{i=1}^{n}m_{_{i}}v_{_{i}}\,\mathrm {d} s_{_{i}}\,\,,}
где {\displaystyle A} и {\displaystyle B} — две конфигурации системы,
{\displaystyle m_{i},\;v_{i}} и {\displaystyle \mathrm {d} s_{i}} —
соответственно масса, алгебраическая скорость и элемент дуги траектории
{\displaystyle i} -й точки, {\displaystyle n} — число точек.
В результате в науку вошёл принцип Мопертюи — Эйлера — первый в ряду
интегральных вариационных принципов механики; позднее данный принцип был
обобщён Ж. Л. Лагранжем, и теперь его обычно трактуют как одну из форм
(форма Мопертюи — Эйлера, рассматриваемая наряду с формой Лагранжа и формой
Якоби) принципа Мопертюи — Лагранжа. Несмотря на свой определяющий вклад, в
возникшей вокруг принципа наименьшего действия дискуссии Эйлер решительно
отстаивал приоритет Мопертюи и указывал на основополагающее значение этого
принципа в механике. Данная идея привлекла внимание физиков, которые в
XIX—XX веках выяснили фундаментальную роль вариационных принципов в природе
и применили вариационный подход во многих разделах своей науки.
Ряд работ Эйлера посвящён вопросам механики машин. В мемуаре «О
наивыгоднейшем применении простых и сложных машин» (1747) Эйлер предложил
вести изучение машин не в состоянии покоя, а в состоянии движения. Этот
новый, «динамический» подход Эйлер обосновал и развил в мемуаре «О машинах
вообще» (1753); в нём он впервые в истории науки указал на три составные
части машины, которые в XIX веке были определены как двигатель, передача и
рабочий орган. В мемуаре «Принципы теории машин» (1763) Эйлер показал, что
при расчёте динамических характеристик машин в случае их ускоренного
движения нужно учитывать не только силы сопротивления и инерцию полезной
нагрузки, но и инерцию всех составных частей машины, и даёт (применительно
к гидравлическим двигателям) пример такого расчёта.
Эйлер занимался также и прикладными вопросами теории механизмов и машин:
вопросами теории гидравлических машин и ветряных мельниц, исследованием
трения частей машин, вопросами профилирования зубчатых колёс (здесь он
обосновал и развил аналитическую теорию эвольвентного зацепления). В 1765
году он заложил основы теории трения гибких тросов и получил, в частности,
формулу Эйлера для определения натяжения троса, используемую и сейчас при
решении ряда практических задач (например, при расчёте механизмов с гибкими
звеньями).
С именем Эйлера связано и последовательное введение в механику идеи
континуума, в соответствии с которой материальное тело представляют,
абстрагируясь от его молекулярного или атомного строения, в виде
непрерывной сплошной среды. Модель сплошной среды была введена Эйлером в
мемуаре «Открытие нового принципа механики» (доложен в 1750 году Берлинской
академии наук и опубликован в её «Мемуарах» двумя годами позже).
В основу рассмотрения автор мемуара положил принцип материальных частиц
Эйлера — положение, приводимое и сейчас во многих учебниках механики и
физики (нередко без упоминания имени Эйлера): сплошное тело с любой
степенью точности можно моделировать системой материальных точек, разбив
его мысленно на достаточно малые частицы и трактуя каждую из них как
материальную точку. Опираясь на этот принцип, можно те или иные
динамические соотношения для сплошного тела получать, записав их аналоги
для отдельных материальных частиц (по Эйлеру, «телец») и почленно
просуммировав (заменяя при этом суммирование по всем точкам интегрированием
по объёму области, занимаемой телом). Данный подход позволил Эйлеру
обойтись без использования таких средств современного интегрального
исчисления (типа интеграла Стилтьеса), которые ещё не были известны в XVIII
веке.
Опираясь на указанный принцип, Эйлер получил — применяя к элементарному
материальному объёму теорему об изменении количества движения — первый
закон движения Эйлера (позже появился и второй закон движения Эйлера —
результат применения теоремы об изменении момента количества движения).
Законы движения Эйлера фактически представляли собой основные законы
движения механики сплошных сред; для перехода к ныне используемым общим
уравнениям движения таких сред не хватало лишь выражения поверхностных сил
через тензор напряжений (это было сделано О. Коши в 1820-х гг.). Полученные
результаты Эйлер применил при изучении конкретных моделей сплошных тел — и
в динамике твёрдого тела (именно в упоминавшемся мемуаре впервые приводятся
уравнения динамики тела с неподвижной точкой, отнесённые к произвольным
декартовым осям), и в гидродинамике, и в теории упругости.
В теории упругости ряд исследований Эйлера посвящён теории изгиба балок и
стержней; при этом уже в ранних работах (1740-е гг.) он занимается задачей
о продольном изгибе упругого стержня, составляя и решая дифференциальное
уравнение изогнутой оси стержня. В 1757 году в работе «О нагрузке колонн»
Эйлер впервые в истории получил формулу для определения критической
нагрузки при сжатии упругого стержня, положив начало теории устойчивости
упругих систем. Практическое применение данная формула нашла значительно
позже — почти сто лет спустя, когда во многих странах (прежде всего, в
Англии) развернулось строительство железных дорог, потребовавшее проведения
расчётов на прочность железнодорожных мостов; именно в это время инженеры и
приняли на вооружение — после некоторого уточнения — модель Эйлера.
Эйлер является — наряду с Д. Бернулли и Ж. Л. Лагранжем — одним из
основоположников аналитической гидродинамики; здесь ему принадлежит заслуга
создания теории движения идеальной жидкости (то есть жидкости, не
обладающей вязкостью) и решения ряда конкретных задач гидромеханики. В
работе «Принципы движения жидкостей» (1752; опубликована девятью годами
позже) он, применяя свои уравнения динамики элементарного материального
объёма сплошной среды к модели несжимаемой идеальной жидкости, впервые
получил для такой жидкости уравнения движения, а также уравнение
неразрывности. Изучая безвихревое движение несжимаемой жидкости, Эйлер ввёл
функцию {\displaystyle S} (позже названную Г. Гельмгольцем потенциалом
скоростей) и показал, что она удовлетворяет дифференциальному уравнению в
частных производных — так в науку вошло уравнение, ныне известное как
уравнение Лапласа.
Результаты данной работы Эйлер существенно обобщил в трактате «Общие
принципы движения жидкостей» (1755). Здесь он — уже для случая сжимаемой
идеальной жидкости — представил (практически в современных обозначениях)
уравнение неразрывности и уравнения движения (три скалярных
дифференциальных уравнения, которым в векторной записи соответствует
уравнение Эйлера — основное уравнение гидродинамики идеальной жидкости).
Эйлер отметил, что для замыкания данной системы из четырёх уравнений нужно
определяющее соотношение, позволяющее выразить давление {\displaystyle p}
(его Эйлер называл «упругостью») как функцию плотности {\displaystyle q} и
«другого свойства {\displaystyle r} , которое влияет на упругость»
(фактически имелась в виду температура). Обсуждая возможность существования
непотенциальных движений несжимаемой жидкости, Эйлер привёл первый
конкретный пример вихревого её течения, а для потенциальных движений такой
жидкости получил первый интеграл — частный случай известного ныне интеграла
Лагранжа — Коши.
К тому же году относится и мемуар Эйлера «Общие принципы состояния
равновесия жидкостей», в котором содержалось систематическое изложение
гидростатики идеальной жидкости (включая вывод общего уравнения равновесия
жидкостей и газов) и была выведена барометрическая формула для
изотермической атмосферы.
В перечисленных работах Эйлер, записывая уравнения движения и равновесия
жидкости, принимал за независимые пространственные переменные декартовы
координаты текущего положения материальной частицы — переменные Эйлера
(впервые такие переменные в гидродинамике использовал Даламбер). Позднее, в
работе «О принципах движения жидкостей. Раздел второй» (1770) Эйлер ввёл и
вторую форму уравнений гидродинамики, в которой за независимые
пространственные переменные принимались декартовы координаты положения
материальной частицы в начальный момент времени (известные сейчас как
переменные Лагранжа).
Основные достижения в этой области Эйлер собрал в трёхтомник «Диоптрика»
(лат. Dioptrica, 1769—1771). Среди главных результатов: правила расчёта
оптимальных характеристик рефракторов, рефлекторов и микроскопов,
вычисление наибольшей яркости изображения, наибольшего поля зрения,
наименьшей длины инструмента, наибольшего увеличения, характеристик
окуляра.
Ньютон утверждал, что создание ахроматической линзы принципиально
невозможно. Эйлер возразил, что комбинация материалов с различными
оптическими характеристиками может решить эту проблему. В 1758 году Эйлер
после долгой полемики сумел убедить в этом английского оптика Джона
Доллонда, который затем сделал первую ахроматическую линзу, соединив друг с
другом две линзы, изготовленные из стёкол различного состава, а в 1784 году
академик Ф. Эпинус в Петербурге построил первый в мире ахроматический
микроскоп.
Эйлер много работал в области небесной механики. Одной из актуальных задач
в тот период было определение параметров орбиты небесного тела (например,
кометы) по небольшому числу наблюдений. Эйлер существенно усовершенствовал
численные методы для этой цели и практически применил их к определению
эллиптической орбиты кометы 1769 года; на эти работы опирался Гаусс, давший
окончательное решение задачи.
Эйлер заложил основы теории возмущений, позднее завершённой Лапласом и
Пуанкаре. Ввёл фундаментальное понятие оскулирующих элементов орбиты и
вывел дифференциальные уравнения, определяющие их изменение со временем.
Построил теорию прецессии и нутации земной оси, предсказал «свободное
движение полюсов» Земли, открытое сто лет спустя Чандлером.
В 1748—1751 годах Эйлер опубликовал полную теорию аберрации света и
параллакса. В 1756 году он опубликовал дифференциальное уравнение
астрономической рефракции, исследовал зависимость рефракции от давления и
температуры воздуха в месте наблюдения. Эти результаты оказали огромное
влияние на развитие астрономии в последующие годы.
Эйлер изложил очень точную теорию движения Луны, разработав для этого
особый метод вариации орбитальных элементов. Впоследствии, в XIX веке, этот
метод был расширен, применён в модели движения больших планет и
используется до настоящего времени. Таблицы Майера, рассчитанные на основе
теории Эйлера (1767), оказались также пригодными для решения насущной
задачи определения долготы на море, и английское Адмиралтейство выплатило
за неё Майеру и Эйлеру специальную премию. Основные труды Эйлера в этой
области:
«Теория движения Луны», 1753;
«Теория движения планет и комет», 1774;
«Новая теория движения Луны», 1772.
Эйлер исследовал поле тяготения не только сферических, но и эллипсоидальных
тел, что представляло собой существенный шаг вперёд. Он также впервые в
науке указал на вековое смещение наклона плоскости эклиптики (1756), и по
его предложению в качестве опорного был с тех пор принят наклон в начале
1700 года. Разработал основы теории движения спутников Юпитера и других
сильно сжатых планет.
В 1748 году, задолго до работ П. Н. Лебедева, Эйлер выдвинул гипотезу, что
хвосты комет, полярные сияния и зодиакальный свет имеют общим источником
воздействие солнечного излучения на атмосферу или вещество небесных
тел.
Всю жизнь Эйлер интересовался музыкальной гармонией, стремясь дать ей ясное
математическое обоснование. Целью раннего его труда — «Опыт новой теории
музыки» (Tentamen novae theoriae musicae, 1739) — была попытка
математически описать, чем приятная (благозвучная) музыка отличается от
неприятной (неблагозвучной). В конце главы VII «Опыта» Эйлер расположил
интервалы по «степеням приятности» (gradus suavitatis), при этом октава
была причислена ко II (наиболее приятному) классу, а диасхизма — к
последнему, XXVII классу (самый неблагозвучный интервал); некоторые классы
(в том числе первый, третий, шестой) в таблице приятности Эйлера были
пропущены. По поводу этой работы ходила шутка, что в ней слишком много
музыки для математиков и слишком много математики для музыкантов.
На склоне лет, в 1773 году Эйлер прочитал доклад в Санкт-Петербургской
академии наук, в котором в окончательном виде сформулировал своё решетчатое
представление звуковой системы; это представление было метафорически
обозначено автором как «зерцало музыки» (лат. speculum musicae). В
следующем году доклад Эйлера был опубликован в виде небольшого трактата De
harmoniae veris principiis per speculum musicum repraesentatis («Об
истинных основаниях гармонии, представленных через speculum musicae»). Под
названием «звуковой сети» (нем. Tonnetz) эйлерова решётка получила широкое
хождение в немецкой музыкальной теории XIX века.
В 1749 году Эйлер опубликовал двухтомную монографию «Морская наука, или
трактат о кораблестроении и кораблевождении», в которой применил
аналитические методы к практическим задачам кораблестроения и навигации на
море, таким как форма судов, вопросы устойчивости и равновесия, методы
управления движением корабля. Общая теория устойчивости корабля А. Н.
Крылова опирается на «Морскую науку».
В круг научных интересов Эйлера входила и физиология; в частности, он
применял методы гидродинамики к исследованию принципов движения крови в
сосудах. В 1742 году он послал в Дижонскую академию статью о течении
жидкостей в эластичных трубках (рассматривавшихся как модели сосудов), а в
декабре 1775 года представил Петербургской академии наук мемуар «Основы
определения движения крови через артерии». В этой работе анализировались
физические и физиологические принципы движения крови, вызываемого
периодическими сокращениями сердца. Трактуя кровь как несжимаемую жидкость,
Эйлер нашёл решение составленных им уравнений движения для случая жёстких
трубок, а в случае эластичных трубок ограничился лишь получением общих
уравнений конечных движений.
Ученики
Одной из главных задач, поставленных Эйлеру по прибытии в Россию, была
подготовка научных кадров. Среди непосредственных учеников Эйлера:
М. Е. Головин, академик математики.
П. Б. Иноходцев, академик астрономии.
С. К. Котельников, академик математики.
А. И. Лексель, талантливый астроном и математик.
С. Я. Румовский, академик астрономии.
Н. И. Фусс, академик математики.
И. А. Эйлер, старший сын Леонарда Эйлера, талантливый математик.
Некоторые из известных потомков Эйлера
Историки обнаружили всего более тысячи прямых потомков Леонарда Эйлера.
Старший сын Иоганн Альбрехт стал крупным математиком и физиком. Второй сын
Карл был известным врачом. Младший сын Христофор впоследствии был
генерал-лейтенантом российской армии и командиром Сестрорецкого оружейного
завода. Все дети Эйлера приняли русское подданство (сам Эйлер всю жизнь
оставался швейцарским подданным).
По состоянию на конец 1980-х годов историки насчитали около 400 ныне
живущих потомков, около половины из них проживали в СССР.
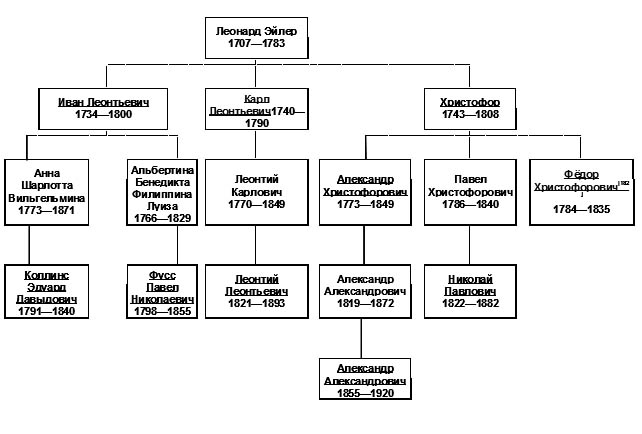
Приведём краткое генеалогическое древо некоторых из известных потомков
Эйлера (фамилия приводится, если она не «Эйлер»).
См. рисунок (Эйлер1 в конце статьи)
Среди других потомков Эйлера: Н. И. Геккер, В. Ф. Геккер и И. Р. Геккер, В.
Е. Скалон, Э. Н. Берендтс. В числе потомков — множество учёных, геологов,
инженеров, дипломатов, врачей, имеются также девять генералов и один
адмирал.
Библиография
Новая теория движения Луны. — Л.: Изд. АН СССР, 1934.
Метод нахождения кривых линий, обладающих свойствами максимума, либо
минимума или решение изопериметрической задачи, взятой в самом широком
смысле. — М.; Л.: Гостехиздат, 1934. — 600 с.
Основы динамики точки. — М.-Л.: ОНТИ, 1938.
Дифференциальное исчисление. — М.-Л.: Геодезиздат, 1949.
Интегральное исчисление. В 3 томах. — М.: Гостехиздат, 1956—1958.
Вариационные принципы механики. Сб. статей: Ферма, Гамильтон, Эйлер, Гаусс
и др / Полак Л. (ред.). — М.: Физматлит, 1959. — 932 с.
Избранные картографические статьи. — М.-Л.: Геодезиздат, 1959.
Введение в анализ бесконечных. В 2 томах. — М.: Физматгиз, 1961.
Исследования по баллистике. — М.: Физматгиз, 1961.
Переписка. Аннотированный указатель. — Л.: Наука, 1967. — 391 с.
Письма к немецкой принцессе о разных физических и философских материях. —
СПб.: Наука, 2002. — 720 с. — ISBN 5-02-027900-5, 5-02-028521-8.
Опыт новой теории музыки (фрагменты трактата) // Музыкальная академия,
1995, № 1, с.140-146.
Опыт новой теории музыки, ясно изложенной в соответствии с непреложными
принципами гармонии. — СПб.: Рос. акад. наук, С.-Петерб. науч. центр,
изд-во Нестор-История, 2007. — ISBN 978-598187-202-0.
Руководство к арифметике для употребления гимназии Императорской Академии
наук. — М.: Оникс, 2012. — 313 с. — ISBN 978-5-458-27255-1.
на латинском языке
Euler Leonhard. Mechanica, sive Motus scientia analytice exposita. 1.
Euler Leonhard. Mechanica, sive Motus scientia analytice exposita. 2.
Euler Leonhard. Tentamen novae theoriae musicae ex certissimis harmoniae
principiis dilucide expositae.
Euler Leonhard. Methodus inveniendi lineas curvas maximi minimive
proprietate gaudentes. — Marc Michel Bousquet, C.
Euler Leonhard. Theoria motuum planetarum et cometarum. — Ambrosius
Haude.
Euler Leonhard. Introductio in analysin infinitorum. 1. — Marc Michel
Bousquet, C.
Euler Leonhard. Introductio in analysin infinitorum. 2. — Marc Michel
Bousquet, C.
Euler Leonhard. Constructio lentium obiectivarum ex duplici vitro. —
Akademija nauk San Pietroburgo.
Euler Leonhard. Institutiones calculi differentialis. 3.
Euler Leonhard. Théorie complete de la construction et de la
manoeuvre des vaisseaux. — Charles Antoine Jombert.
Euler Leonhard. Institutiones calculi differentialis. 1.
Euler Leonhard. Institutiones calculi differentialis. 2.
Euler Leonhard. Institutiones calculi differentialis. 4, Supplementa. —
Akademija nauk San Pietroburgo.
Ссылки: